Exploring The FFT - GF4 As an Educational Tool (Part 1)#
GF4 can be used as an educational tool to explore various corners of data analysis. In this post, we will look at some properties of the Fast Fourier Transform, or FFT. The FFT is a commonly used way to decompose a signal into its frequency components. If you are already familiar with the FFT, none of this will be new, but it may still be interesting to see the various properties materialize before your eyes. If you do not know much about FFTs, it may be interesting and educational. In any case, this post shows the use of some of GF4’s capabilities and commands.
Generate The Curve#
We will not need to load a data file - GF4 will generate the initial data for us. Generate a dampted sine by clicking the button labeled damp Sin:
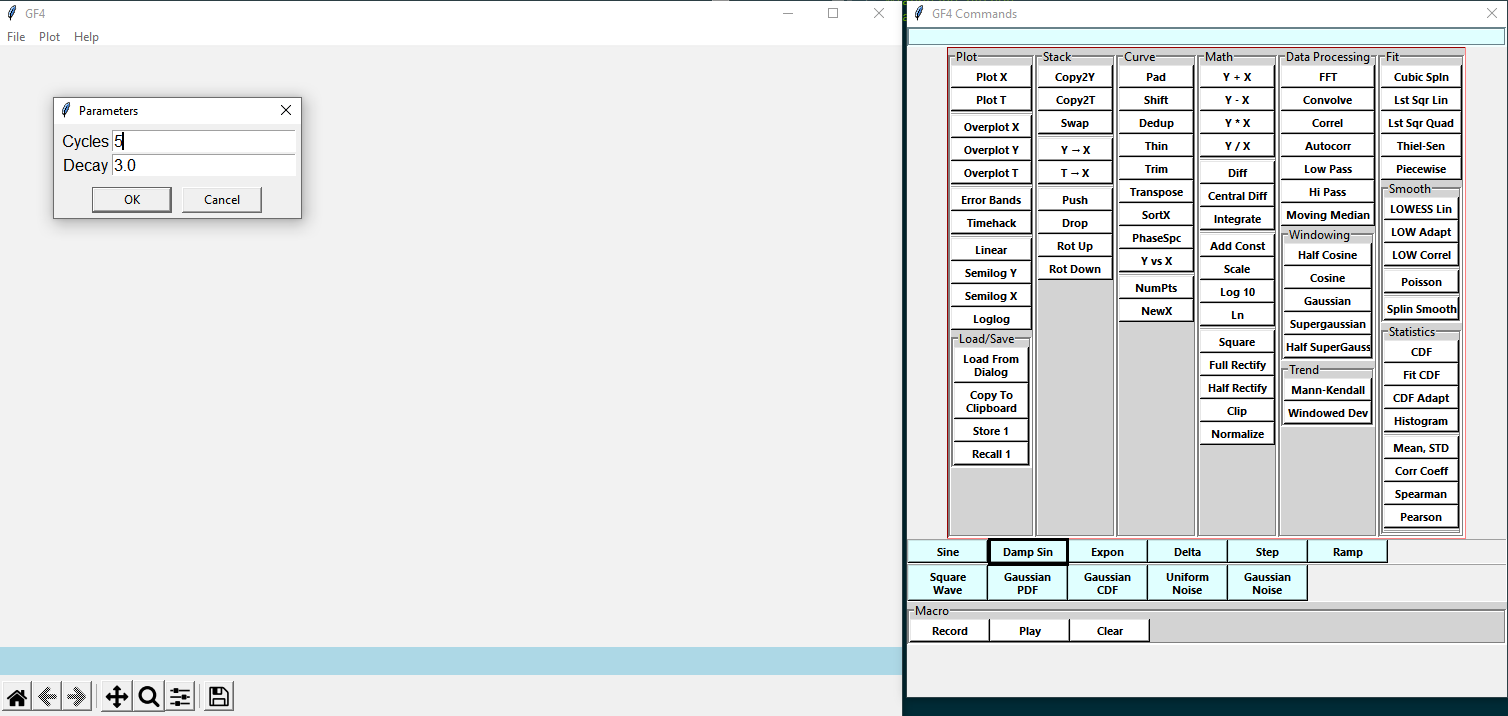
The curve takes two parameters, one for the frequency and one for the damping factor. Accept the defaults by pressing <ENTER>. The damped sine wave will display:
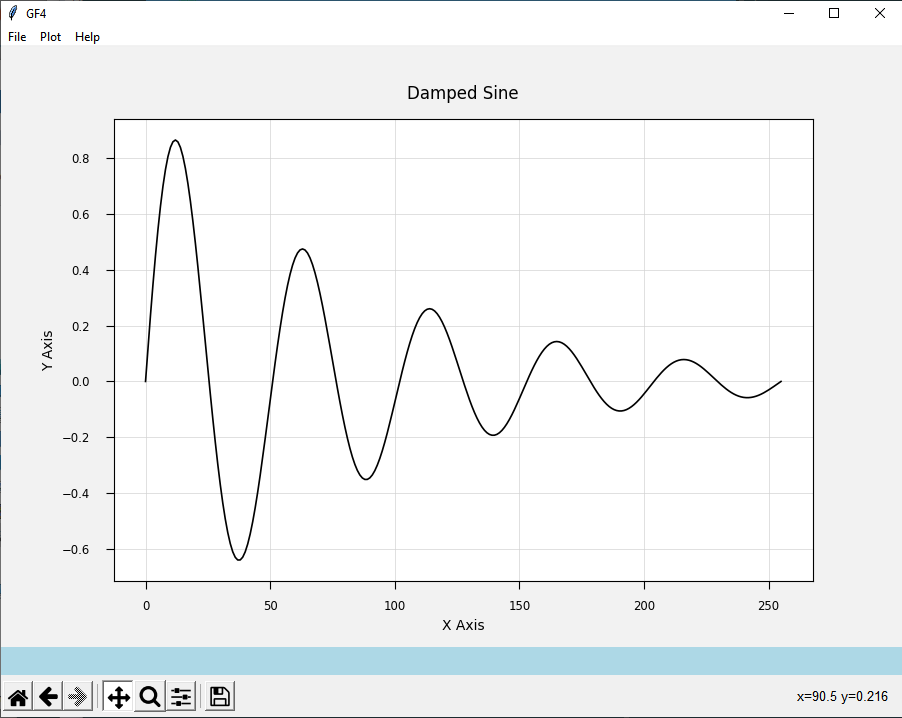
Notice that there are exactly 5 cycles across the graph, as called for in the dialog box.
Change The Number Of Points#
The curve has 5 cycles, but how many points is that? By default, GF4 generates curves of length 256 points. We can check this by clicking on the Pad button:
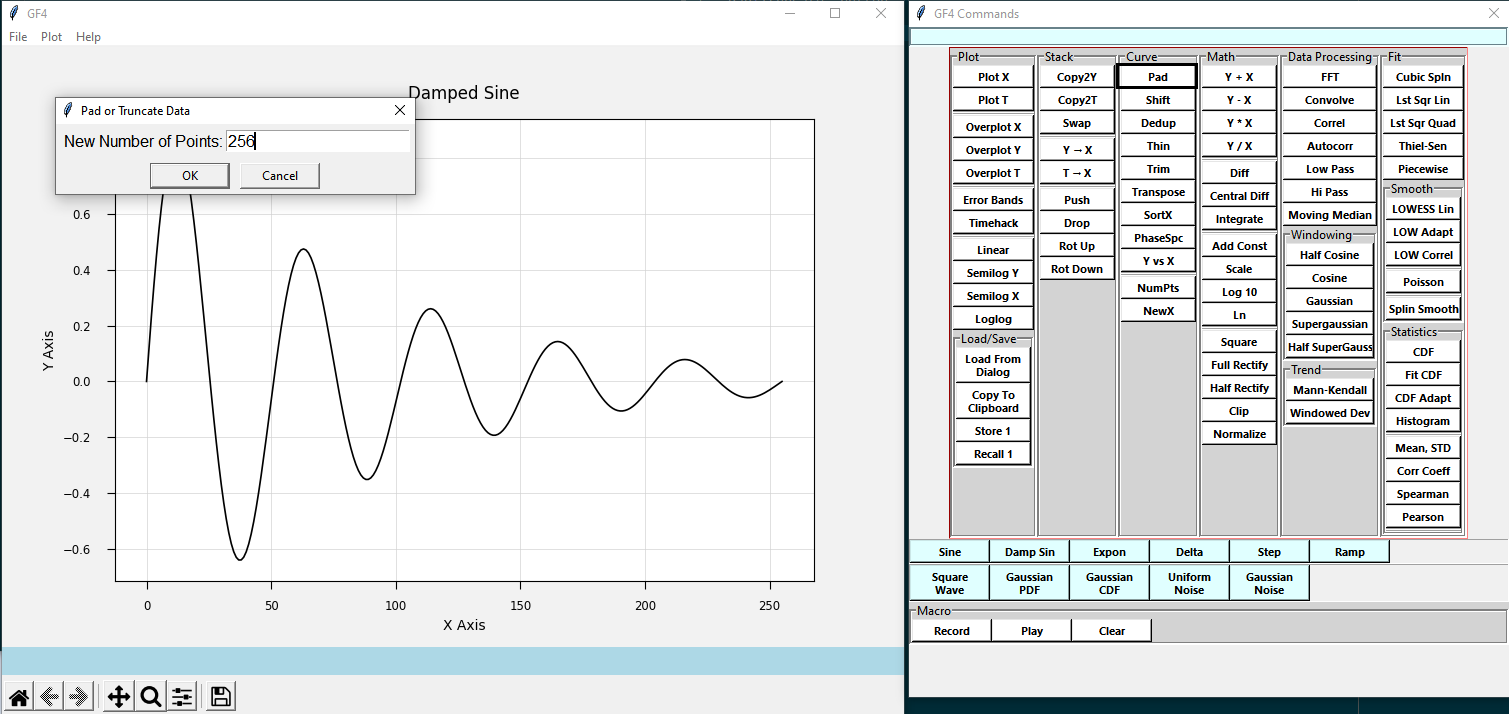
This command shows the length of the curve. It will also allow us to truncate or zero-pad it, but we don’t want to do that here, so Cancel out. Instead, we will change the default number of data points to 1000, a number that will be convenient later.
Click the NumPts button end enter “1000”:
The curve will look the same but now it has 1000 data points.
Cache The Data#
We will want to operate on this curve several times, so save it on the Y and T stack positions by clicking the Copy2Y and Copy2T buttons:

The visible curve is now also stored on both the other stack positions.
Take The FFT#
Next we take the FFT by clicking the FFT button:

Traditionally FFTs require the data set to have an integer power of two points (i.e., 256, 512, etc.) The FFT algorithm used by GF4 can operate efficiently on data of any length. Here is the result:
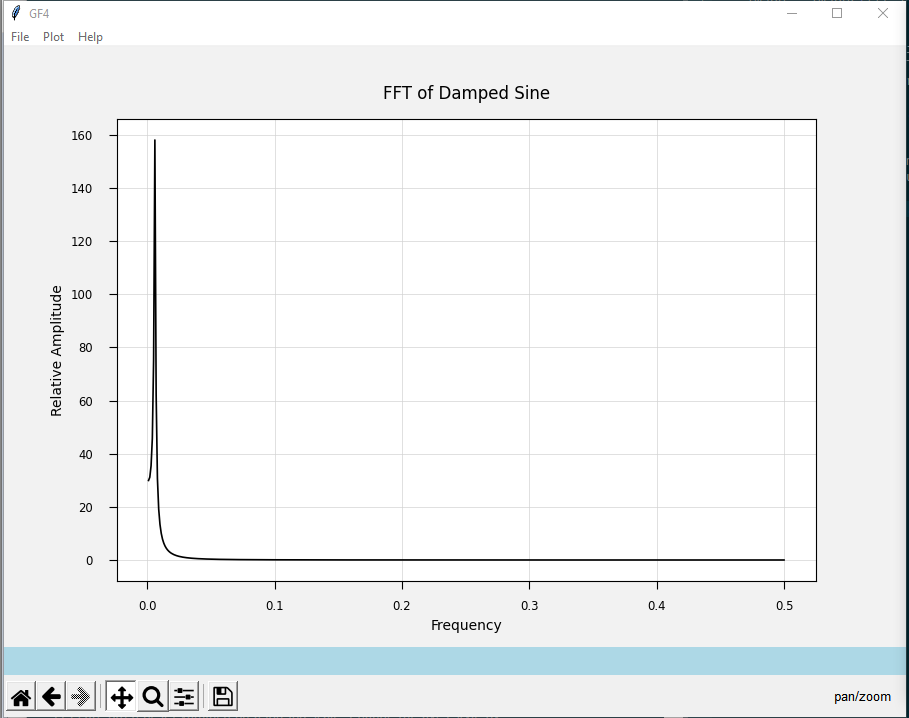
FFTs are often best examined on a log-log scale. Change the axes style by clicking the Loglog button:
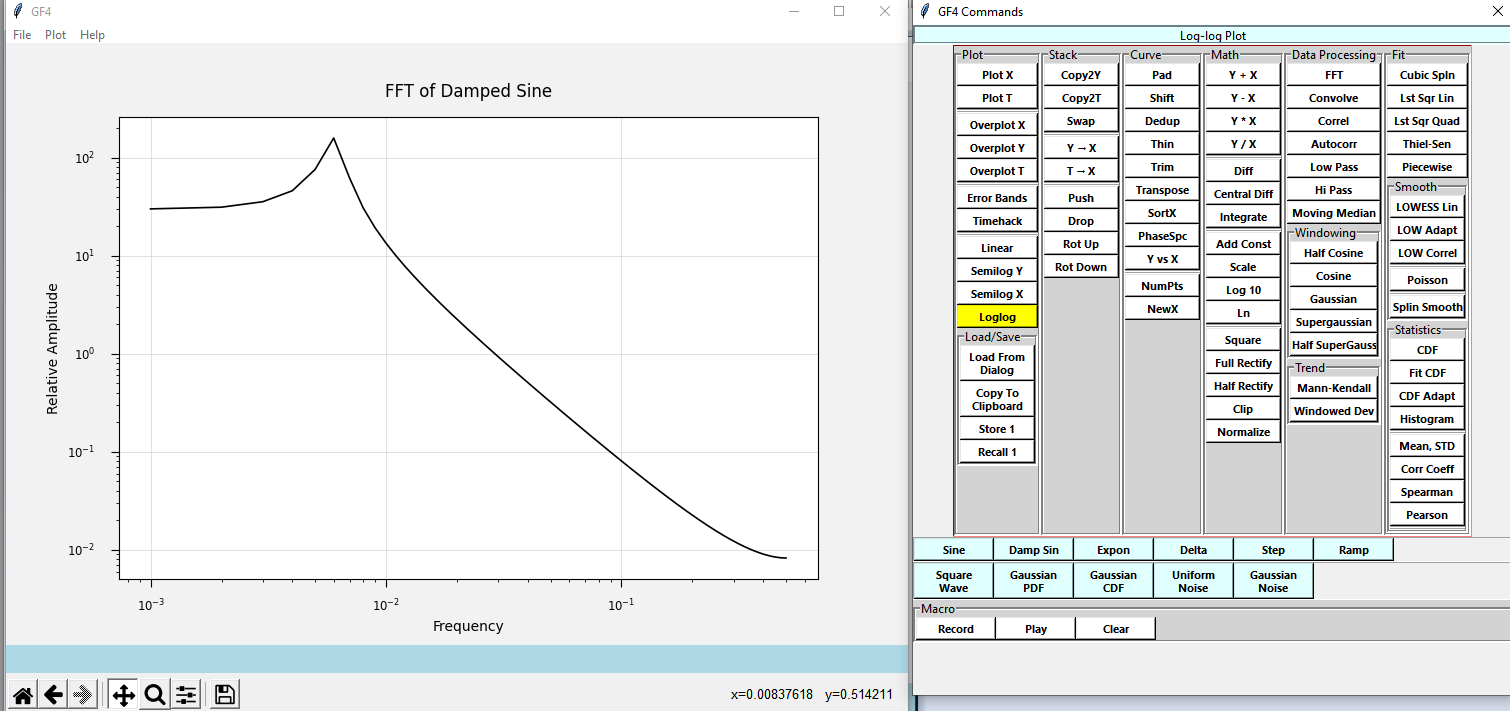
We are almost done for now, but before we close, let us discuss a few aspects of the FFT we have just created.
First notice that there is a single peak. This reflects the frequency we specified when we created the damped sine wave - 5 cycles in 1000 points or 200 points per cycle. Inverting this to get the expected frequency gives 1 / 200 = 0.005. The actual peak is close to this, but there are not enough points to be sure just exactly where the peak is. We will address this next time.
To the left of the peak, the curve levels out at some value. This means that the curve has some power at very low frequencies. This makes sense because every half cycle of a damped sine has a larger peak amplitude than the one following it. So there is a net positive area above the x-axis, and the non-zero low frequency value reflects this fact.
Next Time#
Next time we will investigate the effects of padding and windowing the curve before taking the FFT. We will also add some noise to our so-far-pristine signal.